
Ellis Washington
On Euclid, Archimedes and first principles
By Ellis Washington

*N.B.: This essay is based in part on ideas from Great Books of the Western World, Robert Maynard Hutchins, Editor-in-Chief (1952), Vol. 3, chap. 70 – Principle and Vol. 11 – Euclid and Archimedes
"Give him a coin since he must needs make gain by what he learns."
~ Euclid
Prologue: Biography
Euclid (fl. c. 300 B.C.), also called Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry." He flourished in Alexandria during the rule of Ptolemy I (323–283 BC). His magnum opus, Elements (10 vols.), is one of the most important works in the history of mathematics, and was used as the primary textbook for teaching mathematics (particularly geometry) from the third century B.C. until the early 20th century. In Elements, Euclid deduced the principles of what is now called Euclidean geometry from a small set of axioms ("propositions"). Euclid was indeed a Renaissance man also writing works on perspective, conic sections, spherical geometry, number theory and rigor.
Archimedes of Syracuse (c. 287 BC – c. 212 BC) was an ancient Greek mathematician, engineer, inventor, astronomer, and physicist. Archimedes was born in Syracuse, and perhaps studied in Alexandria, Egypt and later studies with the disciples of Euclid. He spent the rest of his life in Syracuse. Although limited facts of his life are known to us today, he is considered one of the foremost scientists in classical antiquity. Among his pioneering work in physics are the foundations of hydrostatics, statics and an explanation of the principle of the lever. He is recognized with designing advanced machines, including siege engines and the screw pump that today is still used and bears his name (see pictures above). Modern experiments have verified theories that Archimedes designed machines capable of lifting attacking ships out of the water and setting ships on fire using strategic groupings of mirrors reflecting the sun's rays.
Euclid, Archimedes: Why First Principles are critical to preserving knowledge, truth, science, history
The three traditions in which principles are reflected in the canon of the great books are moral principles, principles of action, or political principles. The implication of the word has a dual meaning. Principles as rules of conduct which are used as standards and measures to judge human actions or political events. Either idea regarding principles features certain generalizations. While rules apply to an unlimited number of specific cases, then any principle we appeal to in order to resolve a practical problem or to evaluate the virtues of an action commenced, can by extension be applied again and again in other situations.
Principle, according to its Latin derivation means a beginning or a foundation. Sometimes it means that which comes first absolutely, in the sense of being before everything else; sometimes it means that which comes first only relatively, taking precedence over some things, but having others prior to itself (a priori – "from the earlier").
The historical precedence which belongs to principles in the area of thought, knowledge, justification or even argument, need not be temporal. Principles may possibly be first in the order of learning under first principles. However, if they are not first in the historical order, "they must be first logically, as premises are logically prior to a conclusion, or, as in Euclid's Elements, his principles – his definitions, postulates, and axioms – are logically prior to all the theorems he demonstrates by means of them," according to the writer of the essay on Principle in Great Books.
To Aristotle, principles refers to the method of practical thinking not a means/ends paradigm. He states, we consider neither about the end to be pursued nor about the specific facts on which a choice of the means depends. "The end cannot be a subject of deliberation," he writes, "but only the means; nor indeed can the particular facts be a subject of it, as whether this is bread or has been baked as it should; for these matters of perception." Aristotle's idea of principle is the antithesis of Machiavelli's conception in his famous opus on statecraft, The Prince – "The end justifies the means." – a profoundly skeptical, immoral worldview that in modern times tragically is the predominant political philosophy governing politics, law, economics, education, business, medicine, religion, philosophy, etc.
For example, the Veterans Administration scandal (80% unionized) gave bonuses to high-ranking administrators to not give medical care to needy veterans many of which we are just learning have died waiting for healthcare. Also, VA Secretary Shenseki's resignation Friday was linked to the fact that 1,700 names in the Arizona VA system alone said to be on a "waiting list" that didn't exist.
In the writings of Lucretius two principles are cited as the basic laws of nature – The first is that nothing comes into being out of nothing; the second, that nothing is ever completely reduced to nothingness. The word "principle" is distinguished from the idea of "The One" for Polonius, soul for Plato, matter for Aristotle, or the atoms which Lucretius calls the "first beginnings." Principle to Lucretius applies exclusively to a law – a singular statement of a universal and essential condition which rules over all that is or happens to be (natural law) rather than a specific thing, object, or even to a part of some material being (positive law). From this idea originates the proposition traditionally called "the law of contradiction" – that the same thing cannot both be and not be in the same respect at the same time – is said by Aristotle to be the first principle of being as well as of thought.
Euclid's Elements (Book 1 of 10)
In book one of Euclid's magisterial opus, Elements, following first principles techniques he begins with a few pages of what he refers to as: 'Definitions,' 'Postulates,' and 'Common Notions.' For example:
Secondly, Rationalism – or the view that "regards reason as the chief source and test of knowledge" or "any view appealing to reason as a source of knowledge or justification." More formally, rationalism is defined as a methodology or a theory "in which the criterion of the truth is not sensory but intellectual and deductive." Rationalists believe reality has an intrinsically logical structure. Because of this, rationalists argue that certain truths exist and that the intellect can directly grasp these truths. That is to say, rationalists assert that certain rational principles exist in logic, mathematics, ethics, and metaphysics that are so fundamentally true that denying them causes one to fall into contradiction. Euclidian geometry is indeed more of the rationalist school, however, the a priori reasoning of the empiricists plays a central role in mathematical and scientific theories of both Euclid and Archimedes, but also to America's constitutional Framers, particularly Franklin and Jefferson who were both scientists.
Thus, we see that Euclid and his most famous student, Archimedes, were both methodological Rationalists. Both were obsessed with issues of certainty, deductive reasoning, theory and realizing ever higher forms of learning from first principles.
Archimedes On the Equilibrium of Planes or The Centres of Gravity of Planes (Book One)
Archimedes like Euclid, opens his book with a series of general and self-evident statements of facts he calls, "postulates" and "propositions":
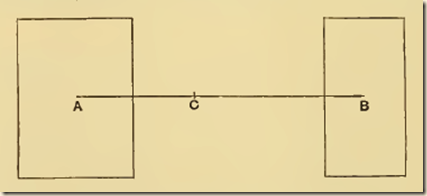
Hence AC<CB. Conversely, if the weights balance, and AC<CB, then A>B. In both the mathematical works of Euclid and Archimedes we find first principles cited throughout these works as a basic, foundational proposition or assumption that cannot be deduced from any other proposition or assumption.
Epilogue: When society abandons First Principles
First principles descends from the idea or ancient notions of how knowledge is acquired and disseminated through the Ages: brick-by-brick; line-by-line; precept-by-precept, idea-by-idea, whereby one writer, philosopher, inventor, intellectual builds upon the work of another; not by destroying, perverting, or "deconstructing" his work but by using first principles, a priori (from the earlier) set forth your paradigm, theory or worldview, and if it is righteous, relevant and true, perhaps it will endure through the Ages as a benefit to humanity until such a time when another writer builds upon the foundation you have laid. Knowledge is thus deductive and its principles can be transferred to other areas of thought which are totally different.
For example, Archimedes proposition on equilibrium above could not only apply to math, but to social relationships. – e.g., two men or two women cannot produce children, therefore this association in society is ipso facto out of balance (lacks equilibrium) with nature (unnatural) and unequal (inferior) to a conventional man/woman pairing.
For Aquinas, as already suggested, the precepts of the natural law are known in the same way as the axioms of theoretical reason. As the truth of the principle of contradiction is known when we understand the meaning of 'is' and 'not' (or 'ought') so that the truth of the first command of natural law – 'Seek the good' – is known when we understand the meaning of 'seek' and 'good.' We hold such truths by the natural habit of our minds (or in Jefferson's words, "We hold these Truths to be self-evident that all men are created equal..."). It is my strong contention that without the legal/political philosophy of natural law which are self-evident truths (laws) in nature given to man by God, that such evil policies as slavery, indentured servitude, and polygamy would never have been abolished in America. Of course I mean in a de jure (legal) sense of the policies in question.
The famous aphorism cited in the epigraph at the very beginning of this essay was attributed to Euclid in answer to a pupil's inquiry at the end of his first lesson in geometry. The precocious student asked the master what he would get by learning such things?- Immediately, Euclid called a slave into the room and said – "Give him a coin since he must needs make gain by what he learns." Thank God Euclid did not subscribe to the politically perverse idea of paying students to learn for the Bible says, Wisdom is justified [proved right] by all of her children. In Euclid's mind those students who had the great privilege to study at his Academy yet did not possess an innate or natural love of learning (philosophy) were therefore equated with the station of slaves and thus paid a slave's wage, ironically by a slave.
In conclusion, what happens to a culture, a society, a nation that abandons first principles? – It loses its collective morality and begins to decay and rot from within. This is what happened to the ancient Greek and Roman civilizations – abandonment of first principles led to widespread societal immorality, decadence, mis-education, corruption and economic collapse, leading to an overreliance of foreign mercenaries to protect and defend its borders, leading to voluntary slavery and finally leading to the historical collapse of once great nations. It happened to ancient Greece and ancient Rome. Can it... (or has it already) happened to America, to Europe, and to the Judeo-Christian traditions of Western Civilization?
Book Notice
Please purchase my latest opus dedicated to that Conservative Colossus, Supreme Court Justice Clarence Thomas. Here are the latest two new volumes from my ongoing historical series – THE PROGRESSIVE REVOLUTION: History of Liberal Fascism through the Ages (University Press of America, 2015):
However, before the book is officially released to the public, I have to place 100 pre-publication orders (50 orders per each volume). I need your help to make this happen ASAP. Please place your order today for Volume 3 & Volume 4. Of course, if you can order all 100 copies today, the book will become official tomorrow.
Please circulate this flyer to all your email contacts & Facebook/Twitter followers who may be interested in purchasing this opus which will serve as a ready apologetic against the rampant Marxist-Progressive propaganda taught in America's public schools, colleges, universities, graduate schools, and law schools. Thanks in advance to all my friends, associates and colleagues for your invaluable support! Law and History Blog: www.EllisWashingtonReport.com
 Invitation for manuscripts
Invitation for manuscripts
I am starting a new a program on my blog dedicated to giving young conservatives (ages 14-35) a regular place to display and publish their ideas called Socrates Corner. If you know of any young person who wants to publish their ideas on any subject, have them send their essay manuscripts to my email at ewashington@wnd.com.
© Ellis Washington
May 31, 2014

*N.B.: This essay is based in part on ideas from Great Books of the Western World, Robert Maynard Hutchins, Editor-in-Chief (1952), Vol. 3, chap. 70 – Principle and Vol. 11 – Euclid and Archimedes
"Give him a coin since he must needs make gain by what he learns."
~ Euclid
Prologue: Biography
Euclid (fl. c. 300 B.C.), also called Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry." He flourished in Alexandria during the rule of Ptolemy I (323–283 BC). His magnum opus, Elements (10 vols.), is one of the most important works in the history of mathematics, and was used as the primary textbook for teaching mathematics (particularly geometry) from the third century B.C. until the early 20th century. In Elements, Euclid deduced the principles of what is now called Euclidean geometry from a small set of axioms ("propositions"). Euclid was indeed a Renaissance man also writing works on perspective, conic sections, spherical geometry, number theory and rigor.
Archimedes of Syracuse (c. 287 BC – c. 212 BC) was an ancient Greek mathematician, engineer, inventor, astronomer, and physicist. Archimedes was born in Syracuse, and perhaps studied in Alexandria, Egypt and later studies with the disciples of Euclid. He spent the rest of his life in Syracuse. Although limited facts of his life are known to us today, he is considered one of the foremost scientists in classical antiquity. Among his pioneering work in physics are the foundations of hydrostatics, statics and an explanation of the principle of the lever. He is recognized with designing advanced machines, including siege engines and the screw pump that today is still used and bears his name (see pictures above). Modern experiments have verified theories that Archimedes designed machines capable of lifting attacking ships out of the water and setting ships on fire using strategic groupings of mirrors reflecting the sun's rays.
Euclid, Archimedes: Why First Principles are critical to preserving knowledge, truth, science, history
The three traditions in which principles are reflected in the canon of the great books are moral principles, principles of action, or political principles. The implication of the word has a dual meaning. Principles as rules of conduct which are used as standards and measures to judge human actions or political events. Either idea regarding principles features certain generalizations. While rules apply to an unlimited number of specific cases, then any principle we appeal to in order to resolve a practical problem or to evaluate the virtues of an action commenced, can by extension be applied again and again in other situations.
Principle, according to its Latin derivation means a beginning or a foundation. Sometimes it means that which comes first absolutely, in the sense of being before everything else; sometimes it means that which comes first only relatively, taking precedence over some things, but having others prior to itself (a priori – "from the earlier").
The historical precedence which belongs to principles in the area of thought, knowledge, justification or even argument, need not be temporal. Principles may possibly be first in the order of learning under first principles. However, if they are not first in the historical order, "they must be first logically, as premises are logically prior to a conclusion, or, as in Euclid's Elements, his principles – his definitions, postulates, and axioms – are logically prior to all the theorems he demonstrates by means of them," according to the writer of the essay on Principle in Great Books.
To Aristotle, principles refers to the method of practical thinking not a means/ends paradigm. He states, we consider neither about the end to be pursued nor about the specific facts on which a choice of the means depends. "The end cannot be a subject of deliberation," he writes, "but only the means; nor indeed can the particular facts be a subject of it, as whether this is bread or has been baked as it should; for these matters of perception." Aristotle's idea of principle is the antithesis of Machiavelli's conception in his famous opus on statecraft, The Prince – "The end justifies the means." – a profoundly skeptical, immoral worldview that in modern times tragically is the predominant political philosophy governing politics, law, economics, education, business, medicine, religion, philosophy, etc.
For example, the Veterans Administration scandal (80% unionized) gave bonuses to high-ranking administrators to not give medical care to needy veterans many of which we are just learning have died waiting for healthcare. Also, VA Secretary Shenseki's resignation Friday was linked to the fact that 1,700 names in the Arizona VA system alone said to be on a "waiting list" that didn't exist.
In the writings of Lucretius two principles are cited as the basic laws of nature – The first is that nothing comes into being out of nothing; the second, that nothing is ever completely reduced to nothingness. The word "principle" is distinguished from the idea of "The One" for Polonius, soul for Plato, matter for Aristotle, or the atoms which Lucretius calls the "first beginnings." Principle to Lucretius applies exclusively to a law – a singular statement of a universal and essential condition which rules over all that is or happens to be (natural law) rather than a specific thing, object, or even to a part of some material being (positive law). From this idea originates the proposition traditionally called "the law of contradiction" – that the same thing cannot both be and not be in the same respect at the same time – is said by Aristotle to be the first principle of being as well as of thought.
Euclid's Elements (Book 1 of 10)
In book one of Euclid's magisterial opus, Elements, following first principles techniques he begins with a few pages of what he refers to as: 'Definitions,' 'Postulates,' and 'Common Notions.' For example:
-
Definitions: 1. A point is that which has no part. 2. A line is breadthless length. 3. The extremities of a line are points. 4. A straight line is a line which lies evenly with the points on itself...
Postulates: 1. To draw a straight line from any point to any point. 2. To produce a finite straight line continuously in a straight line. 3. To describe a circle with any center and distance. 4. That all right angles are equal to one another...
Common Notions: 1. Things which are equal to the same thing are also equal to one another. 2. If equals be added to equals, the wholes are equal. 3. If equals be subtracted from equals, the remainders are equal. 4. Things which coincide with one another are equal to one another. 5. The whole is greater than the part.
Secondly, Rationalism – or the view that "regards reason as the chief source and test of knowledge" or "any view appealing to reason as a source of knowledge or justification." More formally, rationalism is defined as a methodology or a theory "in which the criterion of the truth is not sensory but intellectual and deductive." Rationalists believe reality has an intrinsically logical structure. Because of this, rationalists argue that certain truths exist and that the intellect can directly grasp these truths. That is to say, rationalists assert that certain rational principles exist in logic, mathematics, ethics, and metaphysics that are so fundamentally true that denying them causes one to fall into contradiction. Euclidian geometry is indeed more of the rationalist school, however, the a priori reasoning of the empiricists plays a central role in mathematical and scientific theories of both Euclid and Archimedes, but also to America's constitutional Framers, particularly Franklin and Jefferson who were both scientists.
Thus, we see that Euclid and his most famous student, Archimedes, were both methodological Rationalists. Both were obsessed with issues of certainty, deductive reasoning, theory and realizing ever higher forms of learning from first principles.
Archimedes On the Equilibrium of Planes or The Centres of Gravity of Planes (Book One)
Archimedes like Euclid, opens his book with a series of general and self-evident statements of facts he calls, "postulates" and "propositions":
-
"I POSTULATE the following": 1. "Equal weights at equal distances are in equilibrium, and equal weights at unequal distances are not in equilibrium but incline towards the weight which is at the greater distance."...
Proposition 1: Weights which balance at equal distances are equal. Proposition 2: Unequal weights at equal distances will not balance but will incline towards the greater weight. 3. Unequal weights will balance at unequal distances, the greater weight being at the lesser distance. ...

Hence AC<CB. Conversely, if the weights balance, and AC<CB, then A>B. In both the mathematical works of Euclid and Archimedes we find first principles cited throughout these works as a basic, foundational proposition or assumption that cannot be deduced from any other proposition or assumption.
Epilogue: When society abandons First Principles
First principles descends from the idea or ancient notions of how knowledge is acquired and disseminated through the Ages: brick-by-brick; line-by-line; precept-by-precept, idea-by-idea, whereby one writer, philosopher, inventor, intellectual builds upon the work of another; not by destroying, perverting, or "deconstructing" his work but by using first principles, a priori (from the earlier) set forth your paradigm, theory or worldview, and if it is righteous, relevant and true, perhaps it will endure through the Ages as a benefit to humanity until such a time when another writer builds upon the foundation you have laid. Knowledge is thus deductive and its principles can be transferred to other areas of thought which are totally different.
For example, Archimedes proposition on equilibrium above could not only apply to math, but to social relationships. – e.g., two men or two women cannot produce children, therefore this association in society is ipso facto out of balance (lacks equilibrium) with nature (unnatural) and unequal (inferior) to a conventional man/woman pairing.
For Aquinas, as already suggested, the precepts of the natural law are known in the same way as the axioms of theoretical reason. As the truth of the principle of contradiction is known when we understand the meaning of 'is' and 'not' (or 'ought') so that the truth of the first command of natural law – 'Seek the good' – is known when we understand the meaning of 'seek' and 'good.' We hold such truths by the natural habit of our minds (or in Jefferson's words, "We hold these Truths to be self-evident that all men are created equal..."). It is my strong contention that without the legal/political philosophy of natural law which are self-evident truths (laws) in nature given to man by God, that such evil policies as slavery, indentured servitude, and polygamy would never have been abolished in America. Of course I mean in a de jure (legal) sense of the policies in question.
The famous aphorism cited in the epigraph at the very beginning of this essay was attributed to Euclid in answer to a pupil's inquiry at the end of his first lesson in geometry. The precocious student asked the master what he would get by learning such things?- Immediately, Euclid called a slave into the room and said – "Give him a coin since he must needs make gain by what he learns." Thank God Euclid did not subscribe to the politically perverse idea of paying students to learn for the Bible says, Wisdom is justified [proved right] by all of her children. In Euclid's mind those students who had the great privilege to study at his Academy yet did not possess an innate or natural love of learning (philosophy) were therefore equated with the station of slaves and thus paid a slave's wage, ironically by a slave.
In conclusion, what happens to a culture, a society, a nation that abandons first principles? – It loses its collective morality and begins to decay and rot from within. This is what happened to the ancient Greek and Roman civilizations – abandonment of first principles led to widespread societal immorality, decadence, mis-education, corruption and economic collapse, leading to an overreliance of foreign mercenaries to protect and defend its borders, leading to voluntary slavery and finally leading to the historical collapse of once great nations. It happened to ancient Greece and ancient Rome. Can it... (or has it already) happened to America, to Europe, and to the Judeo-Christian traditions of Western Civilization?
Book Notice
Please purchase my latest opus dedicated to that Conservative Colossus, Supreme Court Justice Clarence Thomas. Here are the latest two new volumes from my ongoing historical series – THE PROGRESSIVE REVOLUTION: History of Liberal Fascism through the Ages (University Press of America, 2015):
However, before the book is officially released to the public, I have to place 100 pre-publication orders (50 orders per each volume). I need your help to make this happen ASAP. Please place your order today for Volume 3 & Volume 4. Of course, if you can order all 100 copies today, the book will become official tomorrow.
Please circulate this flyer to all your email contacts & Facebook/Twitter followers who may be interested in purchasing this opus which will serve as a ready apologetic against the rampant Marxist-Progressive propaganda taught in America's public schools, colleges, universities, graduate schools, and law schools. Thanks in advance to all my friends, associates and colleagues for your invaluable support! Law and History Blog: www.EllisWashingtonReport.com
 Invitation for manuscripts
Invitation for manuscriptsI am starting a new a program on my blog dedicated to giving young conservatives (ages 14-35) a regular place to display and publish their ideas called Socrates Corner. If you know of any young person who wants to publish their ideas on any subject, have them send their essay manuscripts to my email at ewashington@wnd.com.
© Ellis Washington
The views expressed by RenewAmerica columnists are their own and do not necessarily reflect the position of RenewAmerica or its affiliates.
(See RenewAmerica's publishing standards.)


















